Baukasten
Die Anforderungen an ein erstes Teilchen sind also:
- Es enthält einen vollständigen Set aller geometrischen Objekte, aus denen Elementarteilchen entstehen können.
- Es ist symmetrisch und neutral.
- Es ist sein eigenes Anti-Teilchen.
Die Mindestanforderung an ein geometrisches Objekt des Baukastens ist, dass es Teil einer Konfiguration ist, die eine Eigenschaft geometrisch und mathematisch beschreibt.
Die Eigenschaft Masse ist eine implizite Eigenschaft, die sich aus den Vektoren ergibt, die nil bereitstellen muss, um Objekte zu jeweils \(t_{nil} = n + 1\) an Ort und Stelle zu behalten und sie zwingt, sich zu materialisieren, wenn ihre Ausdehnung \(l_{nil} > 0\) ist.
Nimmt man an, dass sich aliq maximal mit \(l_{nil} = 1\) innerhalb von \(t_{nil} = 1\) in nil ausbreiten kann, dann erhält man einen Einheitskreis, eine Einheitssphäre mit \(d = 2_{l_{nil}}\). Spätestens dann muss nil dagegenhalten.
Die einheitliche Objektgrundform, hier Punkt→Kreis→Sphäre, definiert anhand ihrer Oberfläche die elektrische Feldkonstante \(ε_0\) gemäss Dimension. Beim Kreis also \({{\frac {1} {\pi}} r^2}\), bei der Sphäre \({{\frac {1} {4}} {\pi} r^2}\).
Die magnetische Feldkonstante \({\mu_0}\) ist da schon eine Herausforderung. Wir haben einen Bezug zu \(\varepsilon_0\), welches wiederum mit der Ausbreitungsgeschwindigkeit \(c\), in unserem Universum Lichtgeschwindigkeit genannt, zusammenhängt. Und zu \(E\) führt. Wie auch zur Masse \(m\), die Kraft, mit der nil dagegenhalten muss.
Und wir brauchen jede Menge Oberfläche um auf einen annähernden Wert zu kommen. Im Verhältnis zu \({\frac {1} {4}} {\pi} r^2\). Und die Basis sollte ein Quadrat enthalten. Da wir \(c^2\) benötigen. In der jeweils passenden Dimension zu \({\varepsilon_0}\). Rein flächen- und umfangmässig sind Vielecke ergiebiger. Sie sollten aber ein passendes Quadrat enthalten. Hier würden sich rechtwinklige Dreiecke anbieten, die gemäss Pythagoras, \(a^2 + b^2 = c^2\) ergeben. Eine quadratische Fläche basierend auf der Hypothenuse.
Was leider nicht zu dem \({\frac {1} {3}}\) Verhältnis passt, das eine Eigenschaft von Ladung ist. Denn ein gleichseitiges Dreieck hat nun mal überall \(60^{\circ}\). Aber man könnte das gleichseitige Dreieck teilen, erhielte die doppelte Anzahl an rechtwinkligen Dreiecken, die man für \({\frac {1} {3}}\) braucht und somit auch das doppelte Quadrat der Hypothenuse pro Drittel.
Wenn man einen Halbkreis in Drittel aufteilt, der Kreis ist ja schon, um symmetrisch zu sein, in einen positiven und negativen Sektor geteilt, dann ergeben sich 6 Hypothenusen. Da die Fläche der Hypothenuse der Fläche von \(a^2 + b^2\) entspricht, ergibt sich eine Fläche von \(12 r^2\), die bei Ladung 1 abgedeckt würde. Bei Annahme eines Einheitskreises wäre \(c\) dann \({\sqrt{12}}\) in der zweiten reellen Dimension. Wir hätten einen Faktor 4 für die Fläche des gleichseitigen Dreiecks, wenn es in die nächste Dimension erweitert wird. Was keinen Sinn macht. Wir brauchen einen Faktor der ungefähr bei 9 liegt, wenn wir in einer Sphäre sind. Wenn wir im Kreis \({\frac {\pi} {3}}\) wählen, als Representation der minimalsten Drittelfläche, dann müssen wir in der Sphäre \({\frac {4 {\pi}} {3}}\) wählen und noch die Halbkreisflächen addieren, die sich aus der gedrittelten Kugel ergeben. Also \({\frac {4 \pi} {3}} + {\pi}\). Führt aber zu einer zu geringen Lichtgeschwindigkeit insgesamt. Die \({\sqrt{({\frac {4 {\pi}} {3}} + {\pi})}}\) ergibt einen Wert bei 2.7, nicht bei 8.98.
Wenn man die Sechstelkonfiguration anschaut, als Ladung und Anti-Ladung, ergibt sich auch ein Drittel Oberfläche der Sphäre und 2 Kreisflächen, was \({\frac {4 \pi} {3}} + 2{\pi}\) entspräche und einen zu hohen Wert liefert.
Wenn man allerdings berücksichtigt, dass ein magnetisches Feld senkrecht zur Bewegungsrichtung der Ladung und den Feldlinien des Magnets steht, dann muss eine Ladungskonfiguration dies berücksichtigen. D.h. um eine Ladung eines Elementarteilchens korrekt darzustellen, braucht es mindestens zwei Kreisflächen die senkrecht zueinander stehen. Die eine Kreisfläche muss die Beschreibung der Ladungsstärke und Bewegungsrichtung der Ladung enthalten, die andere die Ausbreitungsmöglichkeit von Feldern elektrischer oder magnetischer Ursache, die senkrecht zur Bewegungsrichtung der Ladung stehen und die Feldstärke beschreiben.
Und irgendwo darin muss das Quadrat mit \(a = ({\varepsilon_0} \times {\mu_0})\) liegen, dessen Wurzel, mit -1 ins Verhältnis gesetzt, die Lichtgeschwindigkeit \(c\) ergibt. Oder auch in der vollständigen Konfiguration mit 1 also drei Dritteln als Ergebnis der Effektüberlagerung aller Drittel.
Alpha Version Ladung
Was haben wir aktuell:
- Zwei \({{\frac {4 {\pi}} {6}}}\) Oberflächen, die sich symmetrisch gegenüberstehen.
- Zwei \({{\frac {4 {\pi}} {6}}}\) Oberflächen, die durch die ersten zwei Oberflächen mittig geschnitten werden.
- Vier Schnittflächen mit Fläche \({\pi}\), die sich schneiden.
- Symmetrische Aussparungen in allen Quadranten.
Ein komplexes Gebilde. Mit Möglichkeiten.
Wir haben eine Gesamtoberfläche, die als Verhältnismass dienen kann, sowohl für eine Drittelladung, wie auch für das Verhalten elektrischer und magnetischer Kräfte im Normfall. Wir wollen ja eichen, die Norm festlegen, ohne zu bestimmen, dass sie immer Norm sein muss, nur das sie erstrebenswert ist.
Wir haben Überlappungen, die sich als Interaktionsräume zwischen Ladungsbewegung und Feld eignen. Wir haben Aussparungen, tote Winkel, Bereiche die Interaktion ausschliessen.
Im Moment haben wir noch keinen Drehimpuls, den bekommen wir aber, wenn wir Spin integrieren.
Die Schwierigkeit ist jetzt, die jeweiligen Räume zuzuordnen. Es bietet sich an, das Strecken, wenn sie in Betracht gezogen werden, geometrisch als Quadrat abgeleitet werden. Die Faktoren, wie 10er Potenzen heben wir uns noch für später auf. Die Basiswerte müssen ohne Potenz zumindest ähnlich sein. Denn die Wechselwirkung zwischen mehreren Eigenschaften ist ja noch nicht im Fokus.
Beta Version Ladung
Ich muss den Ladungsentwurf korrigieren, das Feld muss senkrecht zur Bewegungsrichtung liegen und an den äusseren Polen orientiert sein. Es muss Ladung mittig schneiden. Sonst läuft das induzierte Feld ins Leere. Aber was genau heisst senkrecht zur Bewegungsrichtung. In zwei Dimensionen ist das einfach. \({90^{\circ}}\) auf das Ende des Bewegungsvektors. Aber in drei Dimensionen gibt es zwei Achsen, die in Frage kommen können.
Wenn die Rotation der Feldfläche innerhalb von \({t_{nil} = 1}\) erfolgt, dann wird die jeweilige Ladungsfläche und alle Bewegungsrichtungen von Ladung vollständig, quasi gleichzeitig, abgedeckt. Die Winkelgeschwindigkeit muss damit \({{\omega} = 2{\pi}}\) für \({t_{nil} = 1}\) sein.
Die möglichen Reaktionsräume werden hierbei schon reichlich komplex, wenn man die Rotation noch hinzuzieht.
Mit der mittigen Ausrichtung auf den jeweilig vertretenen Kreissegmenten erhält man zusätzlich eine Polung. Die Pole nehmen je nach Anzahl der Kreissegmente eine unterschiedliche Position ein, die jeweils zu \({t_{nil} = n + 1}\) in der Ausgangsposition sind.
Mit der Rotation lässt sich möglicherweise ein Bezug zur Geschwindigkeit herleiten.
Die Umlaufgeschwindigkeit \(v\) der Inkreisfläche, die durch die Dreiecke der Feldkreises bestimmt wird, liefert einen Wert bei 4.7. Die Höhe muss bei 0.5 liegen, da es sich um gleichseitige Dreiecke mit \(a = b = c = 1\) handelt, die den Grosskreis mittig schneiden. \(s\) bezeichnet den Radius des Inkreises. Polarwinkel ist zwingend \({60^{\circ}}\) und ergibt sich aus dem Dreieck das mit \({30^{\circ}}\) anliegt, wobei \(O\) als Mittelpunkt der Sphäre definiert ist. \(r_1\) entspricht \(r_{\perp}\) und es gilt \(v = {\omega}r_{\perp}\).
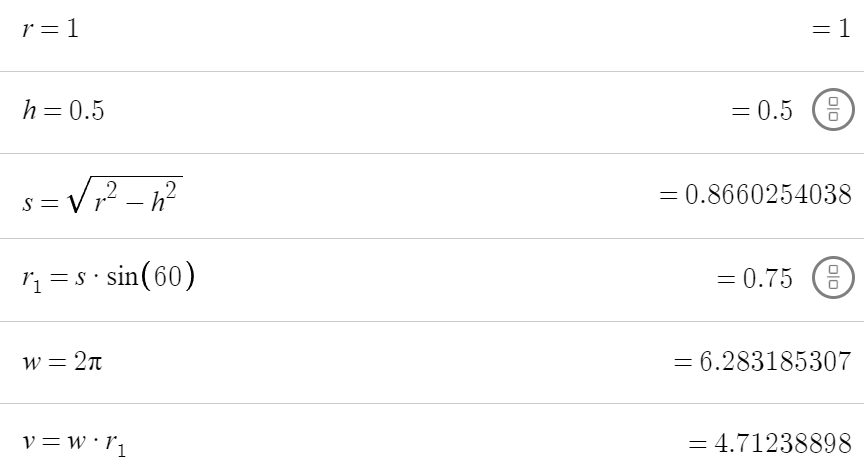
Der Inkreis wäre zumindest stabil, unabhängig von der Anzahl oder dem Vorzeichen der Drittelsegmente des Halbkreises. \(r\) wäre ein Faktor, der die tatsächliche Umlaufgeschwindigkeit beeinflussen könnte. Wenn wir vereinfacht annehmen, dass sich die Vektoren der zwei Inkreise addieren, da sie ja dieselbe Bewegungsrichtung haben, dann kommen wir auf einen Wert von 9.4, der erstmal viel zu hoch, aber halbwegs plausibel für die Baukasteneigenschaft Ladung scheint.
Allerdings fehlt noch Spin und Farbladung, die durchaus einen Einfluss haben könnten und die in dem Modell untergebracht werden müssen ohne das Flächen aufeinander zu liegen kommen. Da wir bereits eine Rotation haben wird es schwierig, da alle Achsen bereits abgedeckt sind. Es wird eng.
Wohin mit dem Spin
Wie könnte die Eigenschaft Spin aussehen, selbst wenn wir noch keinen Platz dafür haben? Das einfachste wäre zwei Halbkreise oder Halbkugeln, die je nach Rotationsrichtung die Werte \(0\), \({\frac {1} {2}}\), \(1\) oder \(-0\), \(-{\frac {1} {2}}\), \(-1\) annehmen können. Aber damit gäbe es keinen Möglichkeit für Antispin und Aufhebung. Die Basis Halbkreis für die Konstruktion macht prinzipiell Sinn aus Symmetrie-Gesichtspunkten. Also bietet sich ein Inkreis-Quadrat an.
Wenn wir uns diese Grundstruktur ansehen, dann ist gleich klar, dass wir es mit Flächen zu tun bekommen, die mit anderen Flächen kollidieren werden. Selbst wenn wir den Kreis um \(45^{\circ}\) rotieren. Wir könnten maximal zwei Segmente vor Kollisionen bewahren. Die anderen zwei werden sich überschneiden mit dem Ladungsfeld oder der Ladung. Egal welches Quadrat wir einzeichnen.
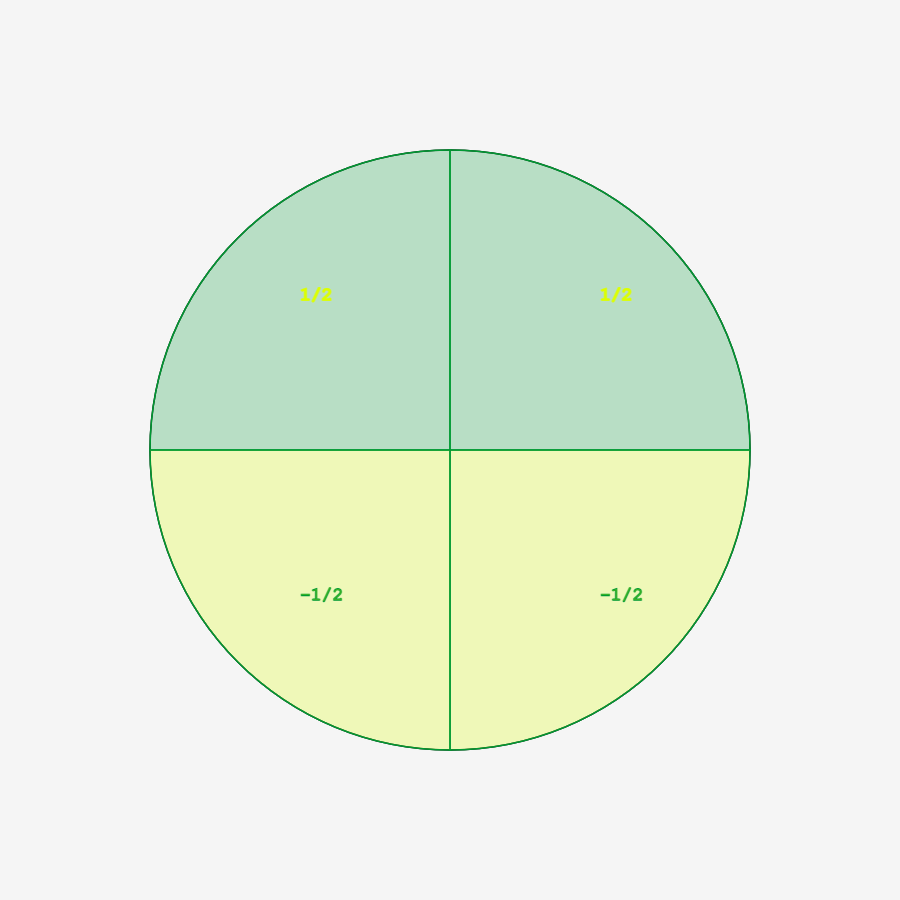
Die nachfolgende Konfiguration wäre gegebenenfalls integrierbar, aber die Argumentation wird ein bisschen haarig, da wir nur \({\frac {1} {2}}\) und \(-{\frac {1} {2}}\) haben. Wo sind \(0\), \(1\) und \(-1\)?
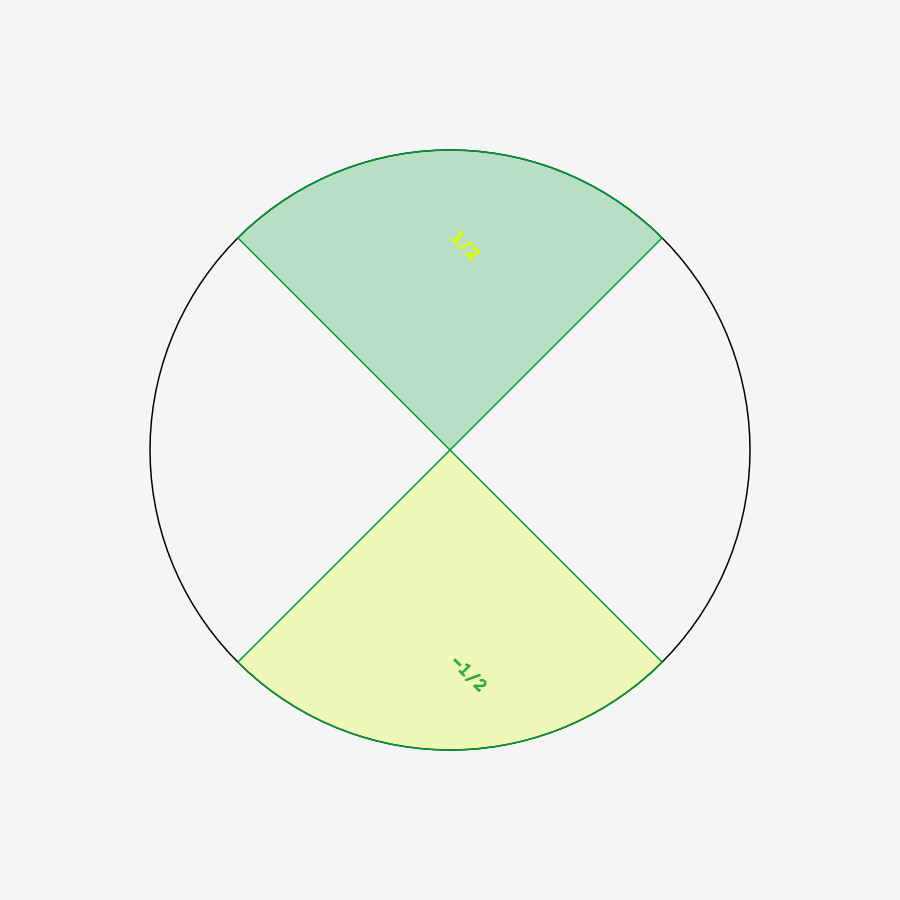
Zudem besteht die Möglichkeit, dass Farbladung eine abgeleitete Grösse aus der Reaktion zwischen Spin und Ladung ist, keine beliebig konfigurierbare Eigenschaft.
Man kann natürlich, wie bei Ladung dieselbe Struktur nochmals senkrecht aufsetzen und mit der geeigneten Rotationsachse wären Interferenzen vermeidbar und man hätte 2 mal \({\pm}{\frac {1} {2}}\). Was Reaktionen nicht ausschliesst, aber Flächen von unterschiedlichen Eigenschaften nicht miteinander kollidieren lässt. Innerhalb einer Eigenschaft ist es wünschenswert, das Flächen miteinander reagieren aber nur minimal, als Schnittpunkte, kollidieren.
Solange Spin um die gleiche Achse rotiert wie das Ladungsfeld, sind Kollisionen unmöglich. Das Spin im gleichen Takt oder in die gleiche Richtung rotieren muss ist noch nicht unbedingt zwingend. Aber wir haben einen geringfügig kleineren Inkreis mit einer anderen Umlaufgeschwindigkeit. Würden uns 8.9 annähern.
Etwas Farbe
Es gibt sogar noch Freiraum der für die Farbladung genutzt werden könnte, allerdings ist der Freiraum symmetrisch auf Basis 2, nicht auf Basis 3. Was entweder bedeuten könnte, es gibt noch zwei unbekannte Farbladungen oder die Aufteilung wird mühsam. Die Segmente müssten in Drittel zerlegt und zugeordnet werden.
Andererseits wäre es ja Verschwendung, den verfügbaren Raum nicht zu nutzen.
Wie es der Zufall will, haben die freien Kreissegmente einen Winkel von \(15^{\circ}\), zufällig die Hälfte eines Sechstelwinkels im Halbkreis oder ein Viertel von \(60^{\circ}\). Es ergibt sich damit eine Beziehung zwischen Basis 2 und Basis 3.
Mit Spin haben wir ja schon eine Turbine. Mit Farbladung könnte man das Gleiche machen, einfach nur mit drei Schnittflächen. Vier kleine Turbinen mit sechs Rotorblättern, die sich erstmal um sich selbst drehen und dann noch zur Achse der Ladung rotieren. Bedeutet aber das jedes Segment einen kompletten Satz von Farbe und Anti-Farbe enthalten kann, das jedes Segment prinzipiell seine eigene Antiteilcheneigenschaft sein kann.
Wenn man den sechsteiligen Kreis auf die Turbine spiegelt, ihm Farben und Anti-Farben zuordnet, die Turbine auch noch rotiert, was heisst, das jede gesetzte Farbe oder Anti-Farbe mit jeder Farbe reagiert, reagieren muss, dann müssen nur noch die Farben übrigbleiben, die sich nicht auslöschen. Was schwieriger ist als es klingt. Denn wir haben zwar Komplementärfarben, die sich gegenseitig auslöschen, aber wenn alle Farben vorhanden sind, sind alle Kombinationen implizit und müssen ergeben, dass sich alle Farben kombiniert mit allen Anti-Farben auslöschen. Ich bezweifle, dass das möglich oder sinnvoll ist.
Wenn dagegen nur halbe Umdrehungen möglich wären, dann würden sich die komplementären Farbeigenschaften während \(t_{nil} = 1\) decken. Es fehlt noch die zündende geometrische Rechtfertigung, warum diese Turbinen anders drehen sollten. Sie hängen an zwei Drehmomenten, wenn sie genau dazwischen sind. Wäre eine Anfangspunkt. Die sind im Moment synchronisiert, rotieren in die gleiche Richtung, allerdings wirkt Spin von oben und Ladung von unten, mit unterschiedlichen Potentialen. Könnte eine Bremsung und Umkippen ab einem gewissen Punkt erklären.
Doch eigentlich müsste es ein Ruckeln ergeben, ein Nachrücken. Die Umlaufgeschwindigkeit der beiden Inkreise ist konstant, die Auftragsfläche ist immer \(r\), also nicht relevant. Die Umlaufgeschwindigkeits-Vektoren laufen also in die Gegenrichtung. Übrig bleibt der Differenzvektor, der das Ruckeln verursachen wird, dass dazu führt, dass Farben, die nicht komplementär sind, aufeinander zu liegen kommen. Wenn man die Vermittlerrolle ernstnehmen will, müssen die Bewegungsmomente von Spin und Ladung die Rotation von Farbladung definieren.
Man könnte natürlich auch sagen, dass diese Eigenschaft die Segmente beschränkt, sie können jeweils nur eine Farbe und Anti-Farbe enthalten und wir haben einen Joker. Eine zusätzliche Kombination, die aus Farbe und Anti-Farbe besteht, aber nicht definiert ist. Was blöd ist, wir sollten wissen, wann welche Farbe und Anti-Farbe im vierten Segment ist. Wir sollten eine Regel haben.
Auch eine Regel für die Verteilung der Farben. Besser wäre es von Frequenzen und Mischfrequenzen zu reden. Die Farbanalogie macht blind.
Farbe bedeutet auch, genau genommen, die Ausnahme von der Regel, dass sich Flächen decken können, da Farbe definiert wie und unter welchen Umständen gedeckte Flächen miteinander reagieren können, ausser sie sind keine Flächen mehr, sondern Schwingungen. Unterhalb \(t_{nil} = 1\) muss alles Schwingung sein, wenn man den Welle-Teilchen-Dualismus umsetzen will.
Was auch bedeuten würde, Flächen können sich überlappen. Die Frage ist, wann man die Situation dafür schafft.
Ziel ist sozusagen die Synthese der Konzepte von Ladung und Spin. Man hat eine kleine Kraft, die nur stark wird, wenn man ihr zu nahe kommt. Und einen Vermittler.
Mit dem Entwurf wäre der Baukasten einigermassen komplett. Es gibt noch Symmetrie-Fragen. So könnte es nicht nur vier, sondern genauso gut acht Farbelemente geben. Ebenso zwei Pol-Ausrichtungen. Das sich acht Komponenten ergeben, passt zumindest zur Theorie, denn eine Eichtransformation wirkt auf ein Fermion \({\psi}\) mit acht reellen Parametern \({\Theta}^{a}\).
Mein Wunsch nach Symmetrie
Wenn das Baukastenteilchen symmetrisch sein soll, dann muss noch etwas an dem Modell geschraubt werden. Mein aktuell präferierter Entwurf spiegelt sowohl das Ladungsfeld, wie auch das Farbladungsfeld.
Regeln aus dem Baukasten
Jetzt kommt der schwierige Teil. Funktioniert es, macht es Sinn und ergeben sich Resultate, die darauf hindeuten, dass es in unserer Welt ähnlich funktioniert?
Die Zutaten sind zumindest simpel. Kreis und mindestens gleichschenklige Dreiecke, sowie gleichseitige Dreiecke. Es können Quadrate abgeleitet werden. Es gibt Reaktionsbereiche und Verbindungen.
Aus den geometrischen Objekten, die in Verwendung sind lassen sich diverse Gesetze für den Baukasten ableiten. Hierbei ist \(r = 1\) nur der maximale Maßstab mit dem geeicht wird. \(r\) kann und muss für einzelne Elementarteilchen kleiner 1 sein. Denn wenn es eine Reaktion geben soll muss es Teilchen und Anti-Teilchen im selben Punktsegment geben. Also kann ein anfängliches Bosonenpaar maximal \(r = {\frac {1} {2}}\) haben.
Für Zeit gilt prinzipiell \(T = 1_{t_{nil}}\), die kleinste Zeiteinheit. Strecken werden in \(l_{nil}\) gemessen. Basiseinheit ist \(L = 1_{l_{nil}}\). Es sind nur Regeln und Abkürzungen gelistet, die sich auf \({\pi}\) oder \(r\) zurückführen lassen, die generellen Regeln für Kreise und Dreiecke gelten weiterhin. Wir haben bis jetzt ja weder eine Lichtgeschwindigkeit, noch ein Caesiumatom um die uns gebräuchlichen SI Maße verwenden zu können.
Einheitskreis
Es gilt: \(r = 1\), \(d = 2\), \(U = 2{\pi}\), \(A = {\pi}\), \({\omega} = 2{\pi}\), Umlaufgeschwindigkeit \(v = {\omega}r\), Polarwinkel \({\vartheta} = 90^{\circ}\).
Kreis
Es gilt: \({r > 0 \wedge r <= 1}: {r \in \mathbb{R}}\), \(d = 2r\), \(U = d{\pi}\), \(A = {\pi}r^2\), Umlaufgeschwindigkeit \(v = {\omega}r_{\perp}\), \({r_{\perp} = r{\sin} {\vartheta}}\).
Gleichseitiges Dreieck
Ladung – Verhältnisse Halbkreis: \({\frac {1} {3}}\), \({\frac {1} {2}}\), Vollkreis: \({\frac {1} {6}}\), \({\frac {1} {4}}\).
Es gilt: \({a = b = c = r}\), \({\alpha} = {\beta} = {\gamma} = 60^{\circ} = {\frac {\pi} {3}}\), \(h = r{\sin}{\frac {\pi} {3}}\), \({A = r{\frac {h}{2}} = {\frac {r^2} {4{\sqrt {3}}}}}\), \(U = 3r\).
Rechtwinkliges gleichschenkliges Dreieck
Spin – Verhältnisse Halbkreis: \({\frac {1} {2}}\), \(1\), Vollkreis: \({\frac {1} {4}}\).
Es gilt: \({a = b = r}\), \({c = r{\sqrt {2}}}\), \({{\alpha} = {\beta} = 45^{\circ} = {\frac {\pi} {4}}}\), \({{\gamma} = 90^{\circ} = {\frac {\pi} {2}}}\), \({h = {\frac {c} {2}}}\), \({A = {\frac {r^2} {2}} = r{\frac {h} {2}}}\), \({U = 2r + c}\).
Gleichschenkliges Dreieck
Farbladung – spezielles Sechstelverhältnis. Ausformung und geometrische Struktur noch fragwürdig.
Es gilt: \({a = b = r}\), \({{\alpha} = {\beta} = 82.5^{\circ} = {\frac {11{\pi}} {24}}}\), \({{\gamma} = 15^{\circ} = {\frac {\pi} {12}}}\), \({h_c = r{\sin}(\alpha)}\), \({c = {\frac {h_c} {\sin {\alpha}}}}\), \({A = c{\frac {h_c} {2}} = r^2{\sin}{\frac {\gamma} {2}}}\), \({U = 2rc}\).
Nächste Schritte
Das ist schon mal was, wir können alle Objekte auf \(r\), bzw. den Wert \(1\) zurückführen. Haben schon einen recht ansehnlichen Baukasten und sind noch nicht einmal bei den Objekten, die sich durch die Kombination ergeben. Ebensowenig bei der symmetrischen Aufteilung und Zuordnung. Oder den Regeln, wie sich die Objekte zueinander verhalten. Im Wesentlichen haben wir Verhältnisse, was es einfach macht über mehrere Dimensionen hinweg. Absolute Werte wären hier hinderlich.
Im symmetrischen Entwurf hat Farbladung acht Attribute und das Ladungsfeld vier Attribute. Diese beiden Komponenten sind in ihrer aktuellen Form noch mit einem grossen Fragezeichen versehen. Besonders Farbladung.